Contens
If you ever had to plot point clouds with more than say ten classes, you’ve probably run into this problem before. You need to assign colors to many classes such that they all appear distinct.
In the simple case, when we have as many classes as colors, this is trivial. But as soon as the number of classes increase, we start running into problems. While there are extended colormaps, even those will run out eventually. After about 20 classes, it becomes very hard to distinguish individual colors.

make_blobs.Why does this problem even exist in the first place? When visualizing data, you’re bound to run into this problem, as the number of classes increases. If you look at e. g. CIFAR-100, then you’re bound to be forced to reuse colors, making it hard to distinguish between different classes.
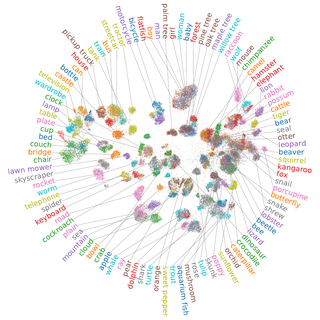
The question now becomes: how can we assign colors to classes such that the confusion between classes is minimized?
Map coloring
One way to think about this is interpreting each class as its own little country. This will then turn the problem of coloring the classes into the problem of coloring a map. How to color different regions in a map has been studied in far greater detail.
Definition: chromatic number
The number of colors (chromas) required to color in a map. The map is viewed as a graph, where all countries are vertices and they share an edge if they share a border. As such, the chromatic number refers to the underlying graph of the map.
The chromatic number for normal maps¹ is proven to be four. So in this case we need to think of a way to draw the “borders” for our “countries” and then we can use the four color theorem to assign the colors without overlap.
As an example, we can generate multiple Gaussian blobs like in the previous image and then look at the decision boundaries of a chosen classifier.

Knowing that we only need four colors to color this in, how do we actually assign the colors to the classes? For this we need to reinterpret the clusters as vertices in a graph. In this graph shared borders will be indicated by an edge, just like in the example given.
For the example given, the class 1 would be connected to the class 7 and 3 (since they share a small border at the bottom). Or the class 9 would be connected to all of its neighbors: 2–4, 6, and 8. The graph can be computed by looking at the response of the decision boundaries and then adding two adjacent responses to the graph.²
Computing the coloring
Now that we have the graph structure, we can start coloring in the classes. For this we will take the following approach. First, we create a matrix with a block diagonal structure, such that each block will correspond to one color choice.

We now have a 9×9 matrix that has three different color slots per color. We want to optimize the color arrangement such that no adjacent classes (indicated by a black square in the adjacency matrix on the left) share a color.
Unfortunately, minimizing the result by permuting the columns of the color matrix is a computationally expensive operation. It corresponds to the quadratic assignment problem, which is NP-hard. Fortunately, we can leverage scipy’s optimization function quadratic_assignment to approximate a possible solution.

The result of this optimization then will give us the columns indices that we can use to finally assign a color to a class. While most colors are assigned properly, the classes 2 and 6 share the same colors but are neighbors. This is one of the compromises that the algorithm has to make since we’re not solving the graph coloring problem directly and we’re using one color less, than required to make the coloring theorem hold.³
By swapping the colors for classes 5 and 6, we could improve the embedding at least a bit. This would still not fulfil the requirement for graph coloring, but in this case the class 6 and 9 would share the same color, and the distance between these two is greater. So how can we encode this notion of distance into the coloring assignment?
Coloring from a confusion matrix
While the binary adjacency matrix works well in some simple cases, it is not sufficient to encode a notion of how close the classes are. Hence, we can use the confusion matrix of the classifier to get an idea of how hard the classes are to distinguish (for the classifier). Higher confusion between the classes means that a distinct color between the two classes is more important.

With this additional signal, the classifier is able to notice that there is more confusion between the classes 2 and 6 than between the classes 6 and 9 and thus the colors are assigned differently.
What’s remarkable (to me) is that the signal of the confusion matrix is weaker than the adjacency matrix, since there are less nonzero entries in the adjacency matrix. Despite this, the coloring actually is better.
Improving the coloring for CIFAR-100
After going through the different steps on the toy example, we can take a look on how it improves things on a proper visualization of the dataset. We can apply the color matching to the t-SimCNE visualization that was shown at the beginning.

While the difference does not look very strong (it’s showing the same data points, there are some different color assignments, where the default setup assigned the same colors, but after the color matching they differ.

Epilogue
The technique is surprisingly useful. While it does not remove all potential confusion, it is a relatively cheap technique that can improve the visualization by reducing confusion.
Code for transforming the old labels to ones that are suitable for coloring can be obtained with the 2D embedding, the old labels (duh), and a classifier of your choice. As a hyperparameter of your choice, you need to decide how many distinct colors you want. As an example, here’s some code:
import numpy as np
from scipy import linalg, optimize
from sklearn import datasets, linear_model, metrics, pipeline, preprocessing
def make_colormat(n_classes, n_colors):
blocksize = int(n_classes / n_colors)
rem = n_classes % n_colors
blocksizes = [blocksize + 1 for _ in range(rem)]
blocksizes += [blocksize for _ in range(n_colors - rem)]
blocks = [np.ones((b, b), dtype=int) for b in blocksizes]
colors = [block for block in blocks]
return linalg.block_diag(*colors)
def match_colors(X, y, clf, n_classes, n_colors):
clf.fit(X, y)
y_pred = clf.predict(X)
confmat = metrics.confusion_matrix(y, y_pred, normalize="true")
colormat = make_colormat(n_classes, n_colors)
optres = optimize.quadratic_assignment(
confmat, colormat, method="2opt", options=dict(rng=1625403879)
)
return optres.col_ind[y]
n_classes, n_colors = 9, 3
X, y = datasets.make_blobs(n_classes * [500], random_state=3609752241)
clf = pipeline.make_pipeline(
preprocessing.StandardScaler(),
linear_model.LogisticRegression(
penalty=None, tol=1e-2, solver="saga", random_state=2862472722
),
)
y_new = match_colors(X, y, clf, n_classes, n_colors)
The steps are as follows:
- Choose a number of colors that you want to use.
- Choose a classifier of your liking.
- Create a color matrix from the number of colors and create the confusion matrix from the classifier.
- Optimize the quadtratic assignment.
- Map the old labels to the new labels, sorted by their color assignment.
Before writing this, I did not know how good the results would be. I was pleasantly surprised to see that this approach works for visualizations I generated without having to change anything. So I will definitely be using this in the future. I hope you find it useful as well.
Footnotes
- Maps without enclaves, which correspond to planar graphs. ↩
- The response is the class label for basically every pixel in the grid of the image. So by iterating over the entire pixel grid, we’re bound to hit the boundary conditions between neighbors. This is not a very efficient method for creating the graph, but it suffices for analysis in 2D. ↩
- The way the problem is introduced differs subtly from the way that we’re trying to solve it. While the graph coloring algorithm is free to choose any color available (that no neighbor has), we are constraining the number of color “slots” before the optimization already. ↩